Das Ergebnis in einem Leistungstest wird mit Normwerten (T-Wert, IQ-Wert usw.) und/oder Prozenträngen festgehalten.
Das Ziel von traditionellen Leistungstests (z. B. Intelligenztests, Rechtschreibtests, Lesetests, Sprachtests, Konzentrationstest, …) besteht darin, einzuschätzen, wie leistungsstark ein getestetes Kind im Vergleich zu Gleichaltrigen, zu Schülerinnen und Schüler der Klassenstufe, zu Kindern mit ähnlichen Voraussetzungen (z.B. zu Mädchen/Jungen, Kindern nicht-deutscher Muttersprache, usw.) ist.

Bei der Überprüfung der speziellen Leistungen wird in standardisierten Tests so vorgegangen, dass den Testpersonen eine Reihe an Aufgaben vorgegeben wird, die in der Regel zunehmend schwieriger werden. Meist können nicht alle Aufgaben gelöst werden. Nach einer bestimmten Fehlerzahl oder einer festgelegten Zeit wird der Testteil abgebrochen. Vorher wird festgelegt, welche Lösungen als richtig und welche als fehlerhaft zu bewerten sind. So kann für jede Testperson ein sogenannter Rohwert berechnet werden. Dieser sagt, wie viele Aufgaben richtig gelöst wurden.

Allerdings ist der Rohwert für die Frage nach dem Leistungsvermögen einer Person nicht aussagekräftig, wenn man nicht weiß, wie viele Punkte andere Testpersonen der Vergleichsgruppe bei diesen Aufgaben erreichen.
In einem sehr leichten Test werden beispielsweise viele Personen einen Großteil der Aufgaben richtig lösen und so einen hohen Rohwert erhalten. Dies spricht dann aber nicht für eine herausragende Leistung, da ja die meisten Testpersonen sehr gut abschneiden. Um die Leistung des Einzelnen ins vergleichen und einschätzen zu können, werden bei der Testentwicklung möglichst große und für die Fragestellung des Tests repräsentative Mengen von Testpersonen untersucht.

Repräsentativ bedeutet dabei vereinfacht ausgedrückt Folgendes: Das zu untersuchende Merkmal (z. B. Intelligenz) ist in dieser Menge etwa so verteilt wie in der Gesamtbevölkerung oder der Personengruppe, für die der Test gelten soll. In der Stichprobe für einen Schultest sollten also nicht nur Schüler aus Begabtenklassen mit vermutlich sehr hoher Intelligenz enthalten sein, sondern auch solche aus Regel- und Förderschulen. Die Anteile der Schüler in der Klasse sollten außerdem den Anteilen in der Bevölkerung entsprechen.
Anhand dieser Stichprobenvergleiche werden der Mittelwert pro Altersgruppe und die Streuungen der Rohwerte in den Altersgruppen bestimmt. Daraus können dann die sogenannten Normwerte berechnet werden. Normwerte sind dabei ein Maßstab, um die individuelle Leistung eines Kindes zu den Ergebnissen der Vergleichsgruppe in Beziehung zu setzen.

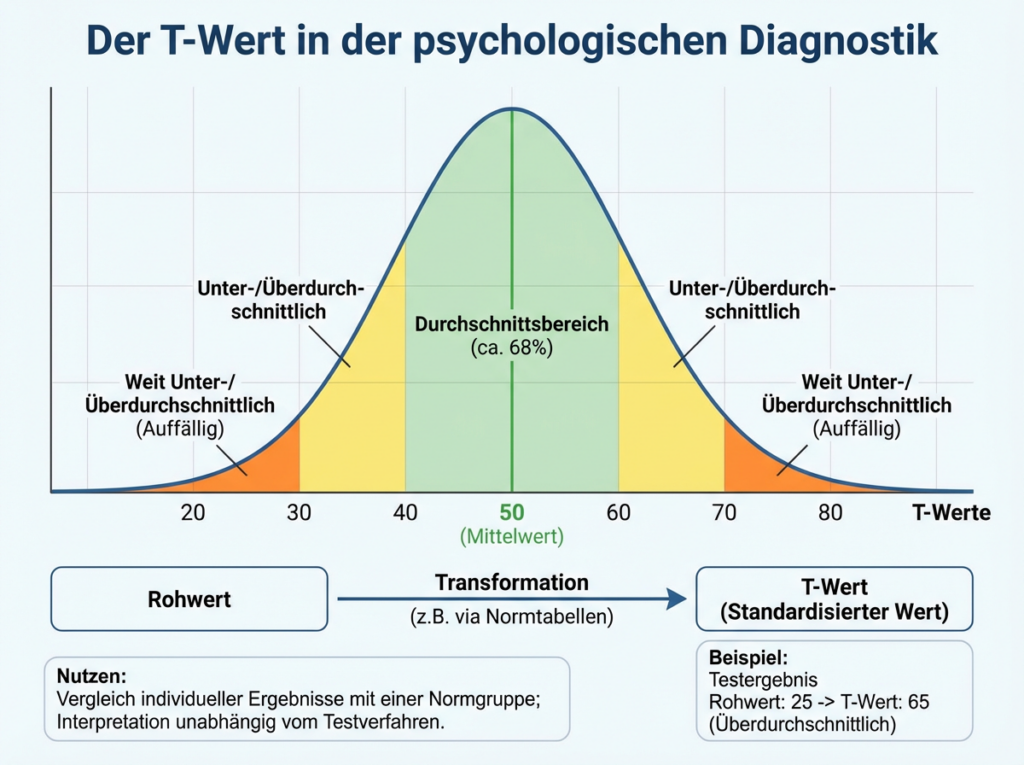
Üblicherweise verwendete Normwerte sind IQ-Werte, T-Werte, Standardwerte, c-Werte, … . Jede dieser Werteskalen weist einen fest definierten Wertebereich auf. Beispielsweise liegt bei den T-Werten der Durchschnittsbereich zwischen 40 und 59 Punkten. Der Mittelwert entspricht einem T-Wert von 50, die Standardabweichung beträgt 10 T-Wert-Punkte.

T-Werte unterhalb von 40 (Mittelwert minus 1 Standardabweichung: 50 – 10 = 40) gelten nach den Festlegungen als unterdurchschnittlich. T-Werte ab 60 (Mittelwert plus 1 Standardabweichung: 50 + 10 = 60) sind als überdurchschnittlich gute Leistung zu bewerten.